Deep Hashing
Hashing BaseLine: https://github.com/willard-yuan/hashing-baseline-for-image-retrieval
Some representative papers about deep hashing
Recent Papers
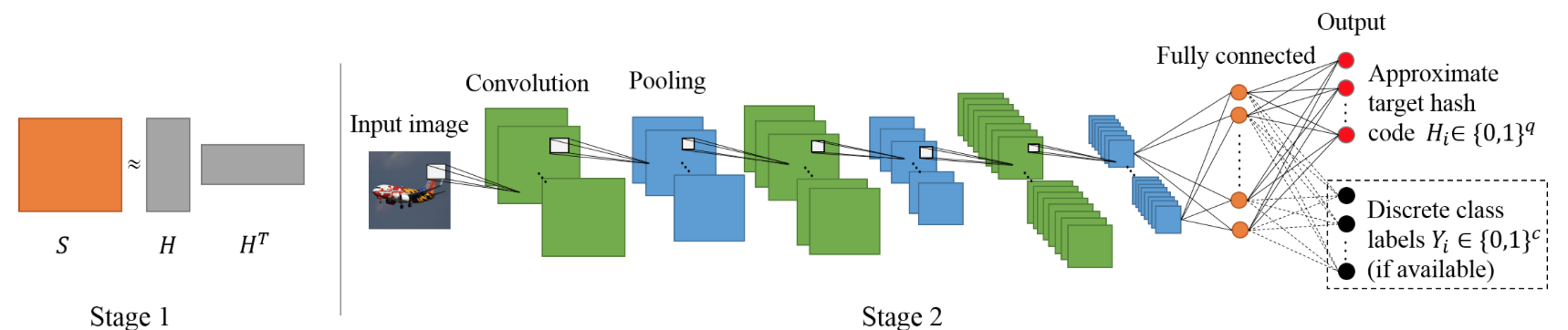
- [x] (CNNH) Supervised Hashing via Image Representation Learning [paper][code][slide]
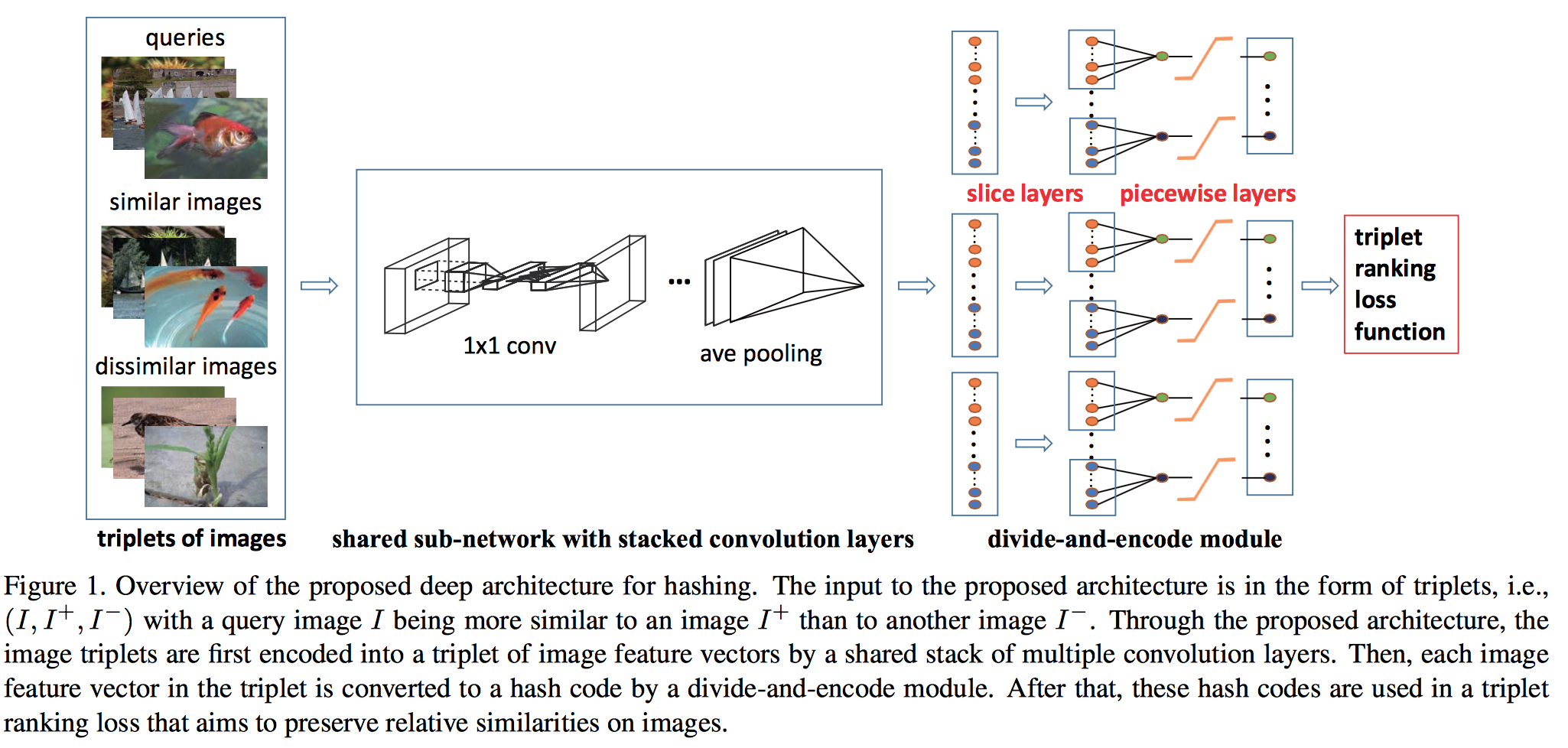
Rongkai Xia, Yan Pan, Hanjiang Lai, Cong Liu, and Shuicheng Yan. [AAAI], 2014 - [ ] (NINH) Simultaneous Feature Learning and Hash Coding with Deep Neural Networks [paper]
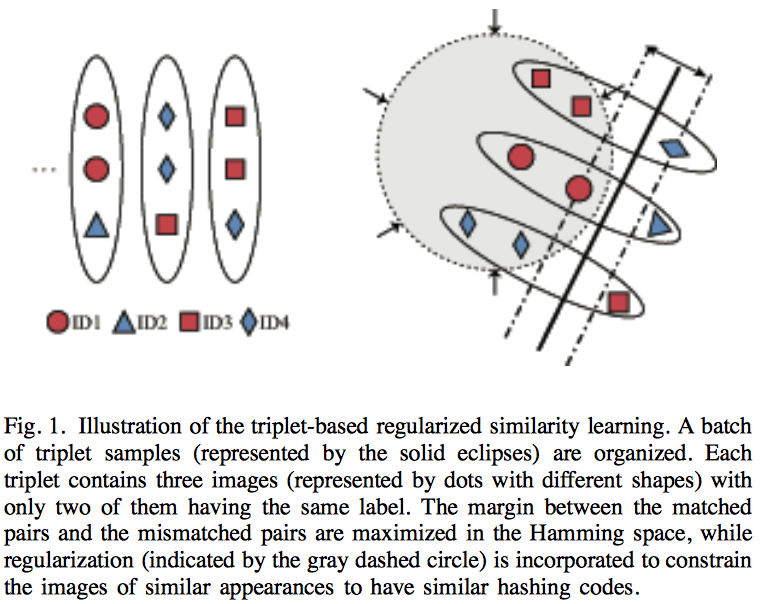
Hanjiang Lai, Yan Pan, Ye Liu, and Shuicheng Yan. [CVPR], 2015 - [ ] (DRSDH) Bit-Scalable Deep Hashing With Regularized Similarity Learning for Image Retrieval and Person Re-Identification [paper][code]
Ruimao Zhang, Liang Lin, Rui Zhang, Wangmeng Zuo, and Lei Zhang. [TIP], 2015 - [ ] Convolutional Neural Networks for Text Hashing [paper]
Jiaming Xu, PengWang, Guanhua Tian, Bo Xu, Jun Zhao, Fangyuan Wang, Hongwei Hao. [IJCAI], 2015 - [x] (DSRH) Deep Semantic Ranking Based Hashing for Multi-Label Image Retrieval [paper][code]
Fang Zhao, Yongzhen Huang, Liang Wang, and Tieniu Tan. [CVPR], 2015 - [x] (DH) Deep Hashing for Compact Binary Codes Learning [paper]
Venice Erin Liong, Jiwen Lu, Gang Wang, Pierre Moulin, and Jie Zhou. [CVPR], 2015 - [x] Deep Learning of Binary Hash Codes for Fast Image Retrieval [paper][code][questions]
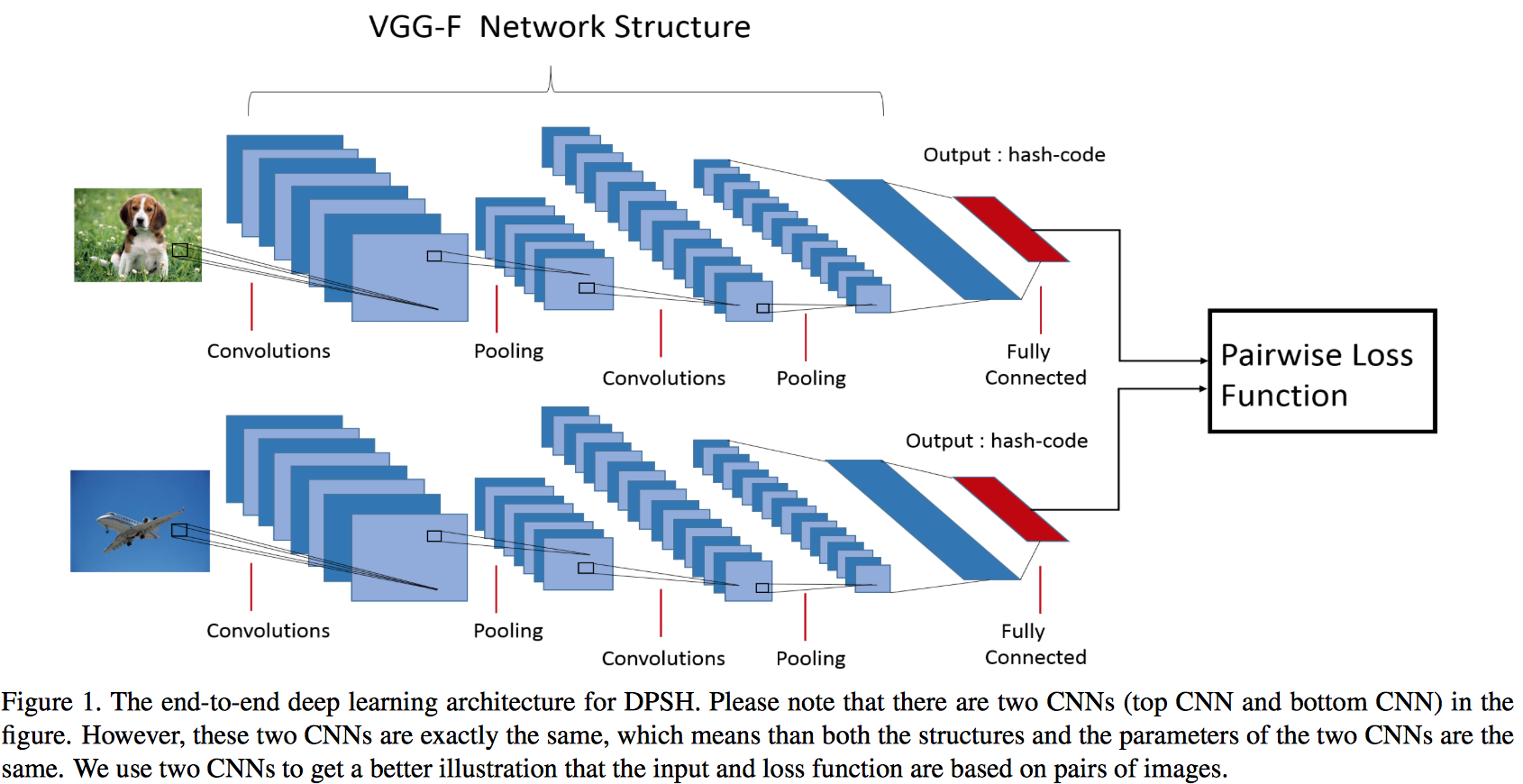
Kevin Lin, Huei-Fang Yang, Jen-Hao Hsiao, and Chu-Song Chen. [CVPRW], 2015 - [x] (DPSH) Feature Learning based Deep Supervised Hashing with Pairwise Labels [paper][code]
- [ ] Deep Learning to Hash with Multiple Representations [paper]
Yoonseop Kang, Saehoon Kim, Seungjin Choi. [ACMMM], 2012 - [ ] Inductive Transfer Deep Hashing for Image Retrieval[paper]
Xinyu Ou, Lingyu Yan, Hefei Ling∗ , Cong Liu, Maolin Liu - [ ] A Deep Hashing Learning Network [paper]
Details
(CNNH) Supervised Hashing via Image Representation Learning [paper][code][slide]
Rongkai Xia, Yan Pan, Hanjiang Lai, Cong Liu, and Shuicheng Yan. [AAAI], 20141.Given the pairwise similarity matrix over training images, they use a scalable coordinate descent method to decompose into a product of where is a matrix with each of its rows being the approximate hash code associated to a training image.

2.In the second stage, the idea is to simultaneously learn a good feature representation for the input images as well as a set of hash functions, via a deep convolutional network tailored to the learned hash codes in and optionally the discrete class labels of the images. (Using Alexnet)
(NINH)Simultaneous Feature Learning and Hash Coding with Deep Neural Networks [paper]
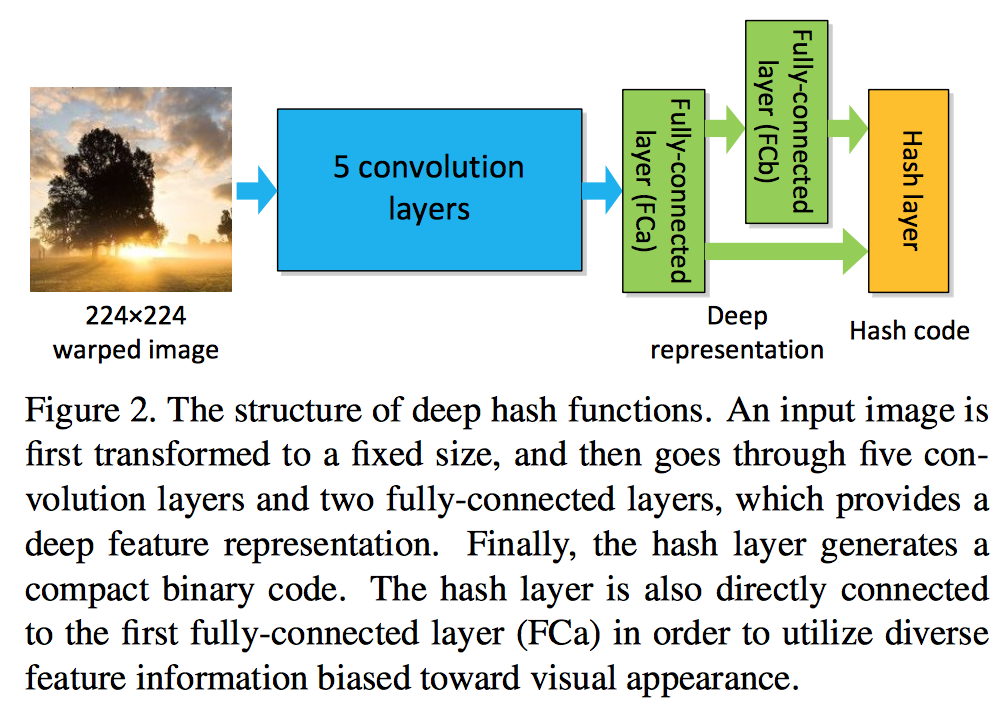
Hanjiang Lai, Yan Pan, Ye Liu, and Shuicheng Yan. [CVPR], 2015The pipeline of the proposed deep architecture consists of three building blocks: 1) a sub-network with a stack of convolution layers to produce the effective intermediate image features; 2) a divide-and-encode module to divide the intermediate image features into multiple branches, each encoded into one hash bit; and 3) a triplet ranking loss designed to characterize that one image is more similar to the second image than to the third one.
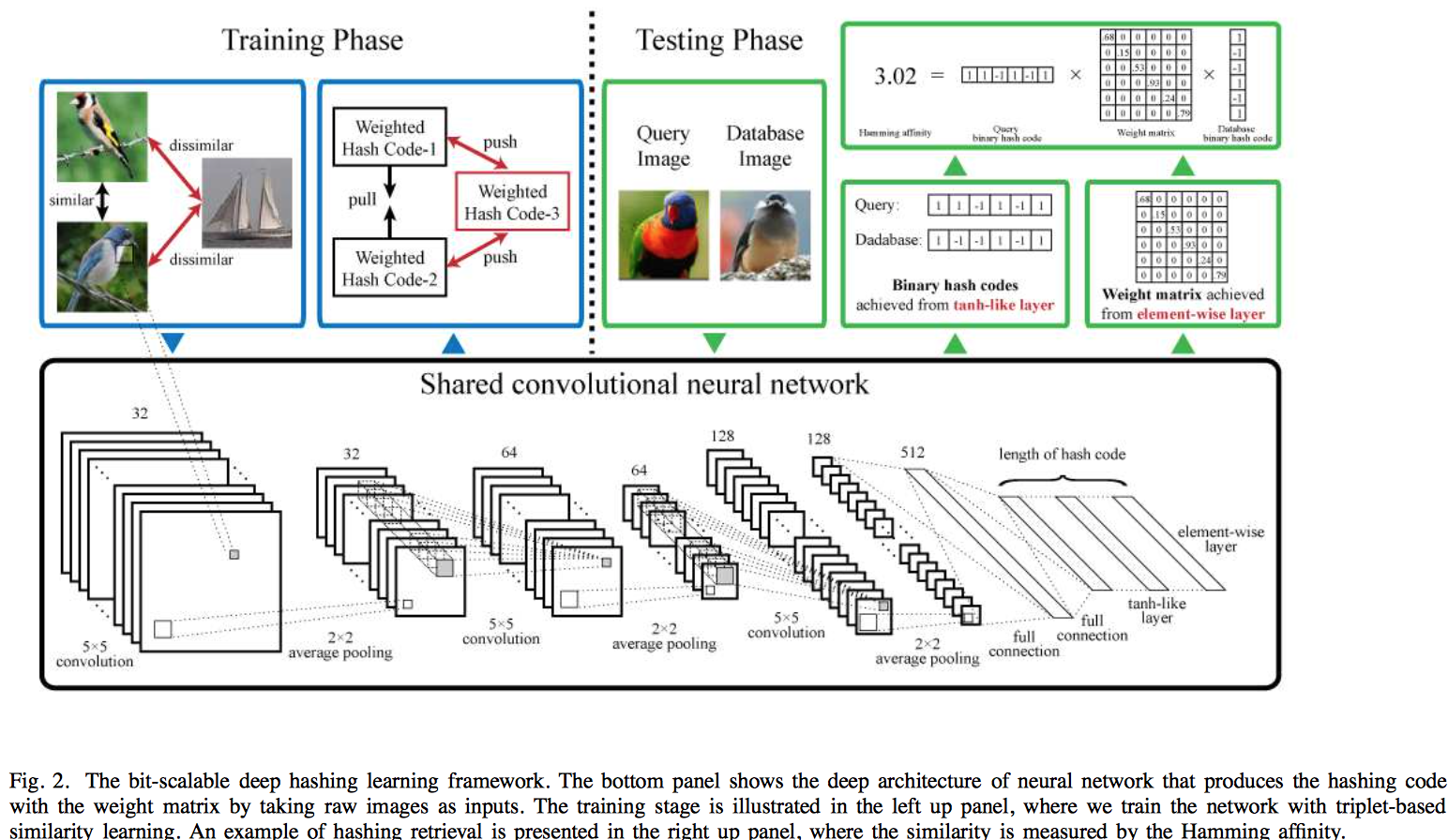
(DRSDH) Bit-Scalable Deep Hashing With Regularized Similarity Learning for Image Retrieval and Person Re-Identification [paper][code]
Ruimao Zhang, Liang Lin, Rui Zhang, Wangmeng Zuo, and Lei Zhang. [TIP], 2015We pose hashing learning as a problem of regularized similarity learning. Specifically, we organize the training images into a batch of triplet samples, each sample containing two images with the same label and one with a different label. With these triplet samples, we maximize the margin between matched pairs and mismatched pairs in the Hamming space. In addition, a regularization term is introduced to enforce the adjacency consistency, i.e., images of similar appearances should have similar codes. The deep convolutional neural network is utilized to train the model in an end-to-end fashion, where discriminative image features and hash functions are simultaneously optimized.
Convolutional Neural Networks for Text Hashing [paper not found]
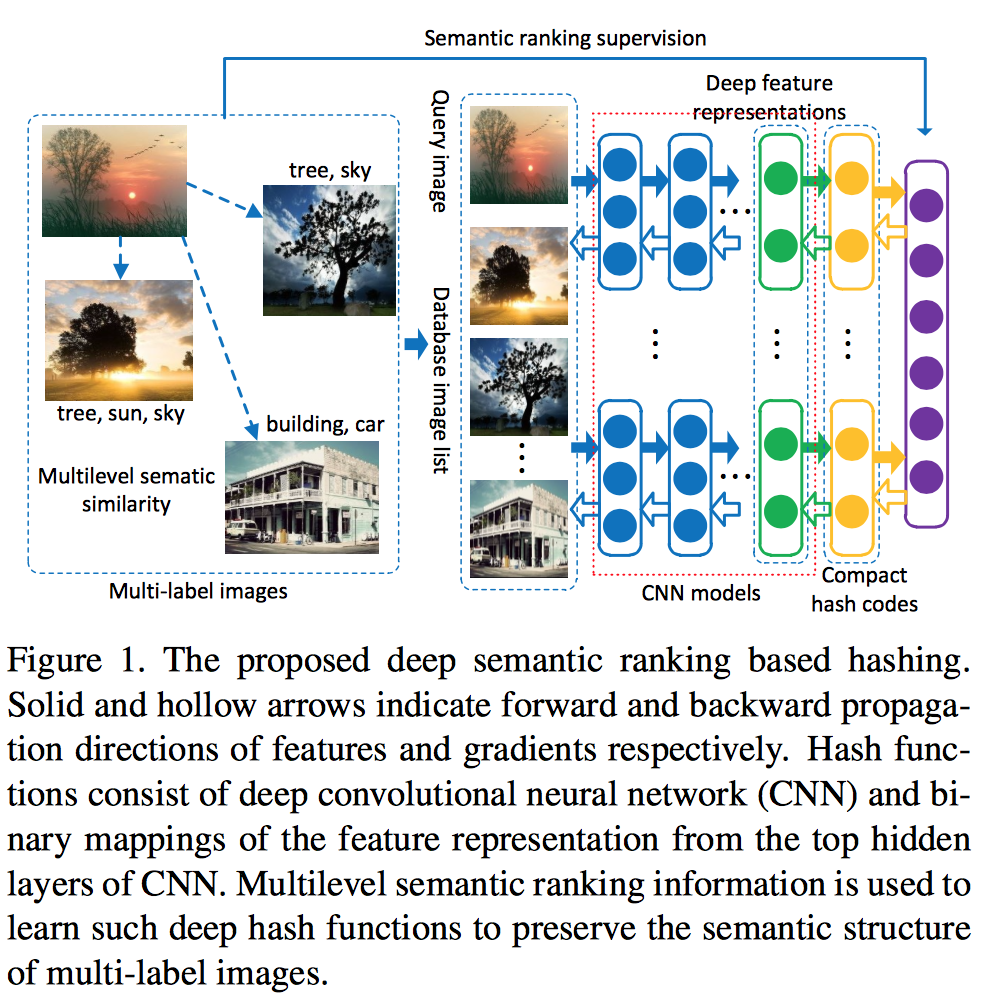
Jiaming Xu, PengWang, Guanhua Tian, Bo Xu, Jun Zhao, Fangyuan Wang, Hongwei Hao. [IJCAI], 2015(DSRH) Deep Semantic Ranking Based Hashing for Multi-Label Image Retrieval [paper][code]
Fang Zhao, Yongzhen Huang, Liang Wang, and Tieniu Tan. [CVPR], 2015Deep convolutional neural network is incorporated into hash functions to jointly learn feature representations and mappings from them to hash codes, which avoids the limitation of semantic representation power of hand-crafted features. Meanwhile, a ranking list that encodes the multilevel similarity information is employed to guide the learning of such deep hash functions. An effective scheme based on surrogate loss is used to solve the intractable optimization problem of non-smooth and multivariate ranking measures involved in the learning procedure.
- Deep Hash Functions:
- Semantic Ranking Supervision: (preserve multilevel semantic structure)various evaluation criteria can be used to measure the consistency of the rankings predicted by hash functions, such as the Normalized Discounted Cu- mulative Gain (NDCG) score: , where is the truncated position in a ranking list, is a normalization constant to ensure that the NDCG score for the correct ranking is one, and is the similarity level of the -th database point in the ranking list.
- Optimization with Surrogate Loss:
Given a query and a ranking list for , we can define a ranking loss on a set of triplets of hash codes as follows: . According to NDCD, weight
The objective function can be given by the empirical loss subject to some regularization:
And calculate derivative values.
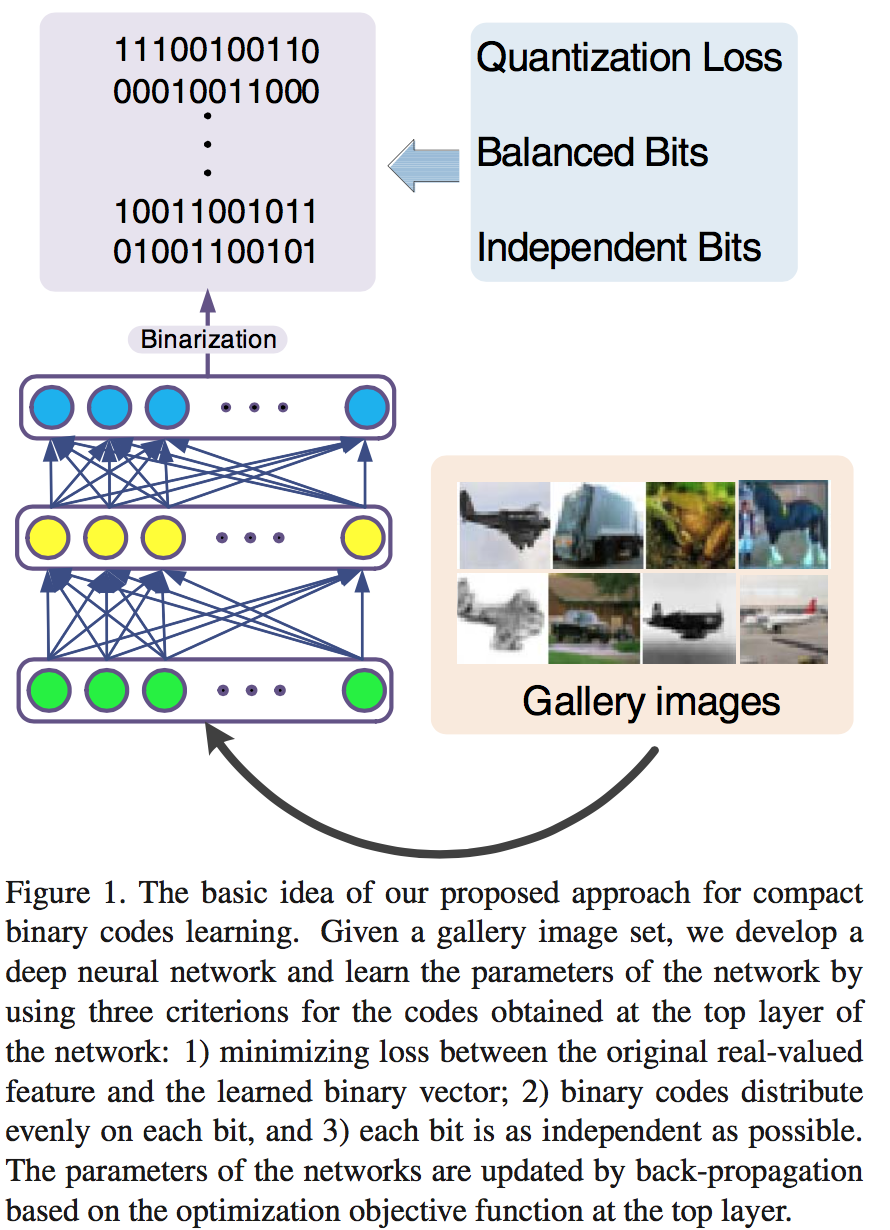
(DH) Deep Hashing for Compact Binary Codes Learning [paper]
Venice Erin Liong, Jiwen Lu, Gang Wang, Pierre Moulin, and Jie Zhou. [CVPR], 2015Our model is learned under three constraints at the top layer of the deep network: 1) the loss between the original real-valued feature descriptor and the learned binary vector is minimized, 2) the binary codes distribute evenly on each bit, and 3) different bits are as independent as possible. To further improve the discriminative power of the learned binary codes, we extend DH into supervised DH (SDH) by including one discriminative term into the objective function of DH which simultaneously maximizes the inter-class variations and minimizes the intra-class variations of the learned binary codes.
- DH Loss function: , where is the quantization loss, is the balance bits constraint, is the independent bit constraint, and are regularizers to control scales of parameters.
- SDH (Supervised): ,
where , , and two sets or from the training set, which represents the positive samples pairs and the negative samples pairs in the training set, respectively.


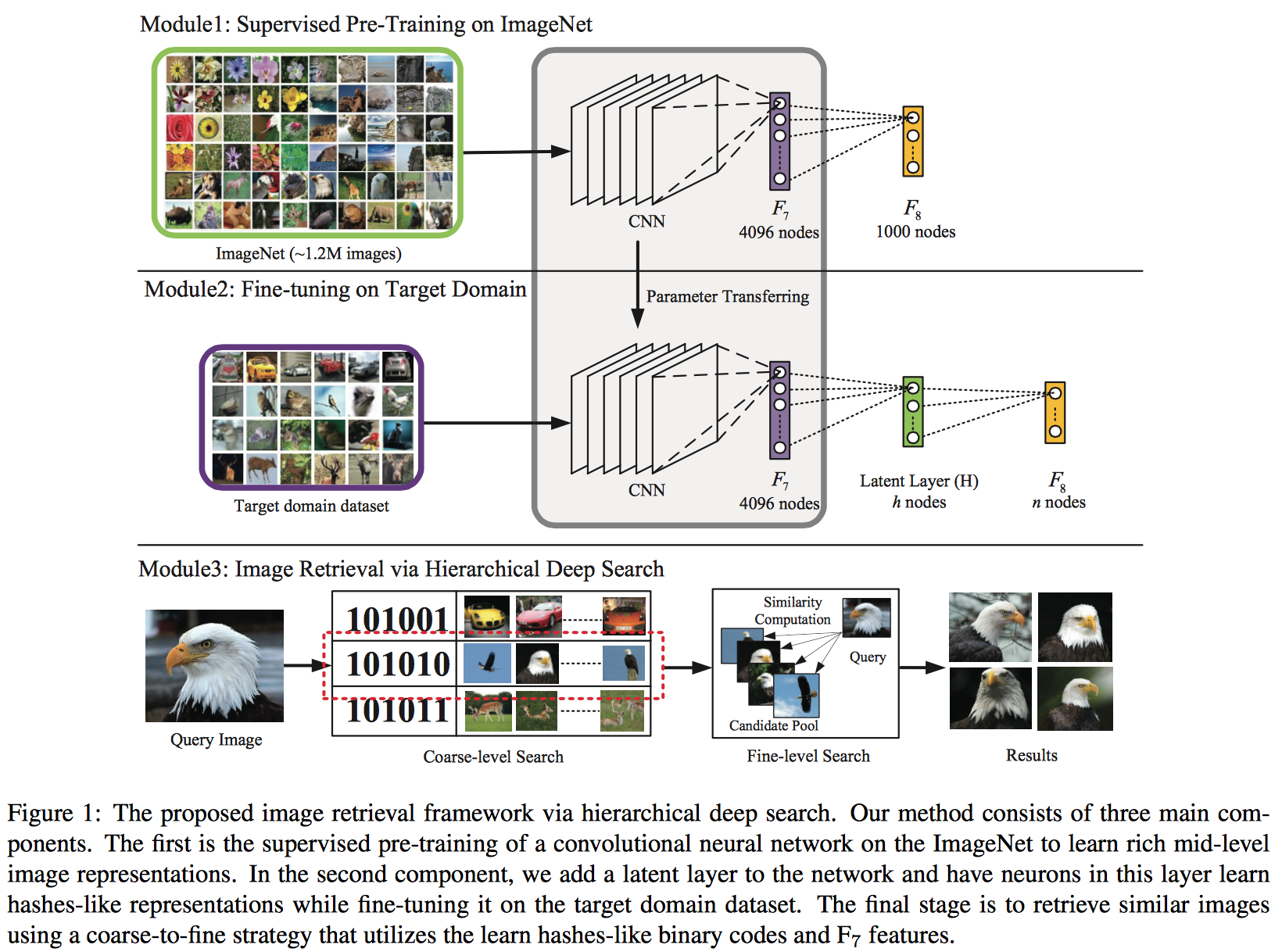
- Deep Learning of Binary Hash Codes for Fast Image Retrieval [paper][code][questions]
Kevin Lin, Huei-Fang Yang, Jen-Hao Hsiao, and Chu-Song Chen. [CVPRW], 2015- Learning Hash-like Binary Codes: Add a latent layer between and to represent the hash code layer. The neurons in the latent layer H are activated by sigmoid functions.The initial random weights of latent layer $H$ acts like LSH.
- Coarse-level Search: The binary codes are then obtained by binarizing the activations by a threshold. (1, if , 0, ). Then we can get a pool of candidates.
- Fine-level Search: Use the euclidean distances of layer feature.
(DPSH) Feature Learning based Deep Supervised Hashing with Pairwise Labels [paper][code]
Wu-Jun Li, Sheng Wang and Wang-Cheng Kang. [arXiv], 2015- Define the pairwise loss function similar to that of LFH: , where
- Compute the derivatives of the loss function with respect to the (relaxed) hash codes as follows: , where with